saowu's Blog

矩阵快速幂求Fibonacci

矩阵快速幂求Fibonacci
2020-04-23 · 8 min read
Java

一、“斐波那契数列”

  • 斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

二、快速幂

快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N)， 与朴素的O(N)相比效率有了极大的提高。

    /**
     * 快速幂（位运算）
     * @param a 底数
     * @param n 指数
     * @return
     */
    public static long quickPow(long a, long n) {
        long tmp = a;
        long ans = 1;
        while (n > 0) {
            if (n % 2 != 0) {
                ans = ans * tmp;
            }
            tmp = tmp * tmp;
            n >>= 1;
        }
        return ans;
    }
  • 例如，在求5^19时，按照普通的求法就是要19个5相乘，这样虽然可以解出来，但当底数和指数都非常大时，这样计算的时间会很长，其时间复杂度为O（n）。但使用快速幂就要快速很多。
    • 其计算原理如下（下面底数用a表示，指数用n表示，下面的tmp初始为a，ans初始为1）
    • n=19的二进制是10011;
    • 此时n=19为奇数，则ans=ans*tmp；tmp=tmp*tmp；n右移一位；
    • （ans=1 * 5，tmp=5 * 5=25）
    • 此时n=9为奇数，则ans=ans*tmp；tmp=tmp*tmp；n右移一位；
    • （ans=5 * 25，tmp=25 * 25=625）
    • 此时n=4为偶数，则tmp=tmp*tmp；n右移一位；
    • （ans=125，tmp=625 * 625=390625）
    • 此时n=2为偶数，则tmp=tmp*tmp；n右移一位；
    • （ans=125，tmp=390625 * 390625）
    • 此时n=1为奇数，则ans=ans*tmp；tmp=tmp*tmp；n右移一位；
    • （ans=125 * 390625 * 390625，tmp=(390625 * 390625)^2）;
  • 这样就已经求解成功，仅仅用了5次，大大节省了时间。其时间复杂度为O（logn）。

三、矩阵快速幂

顾名思义，矩阵快速幂就是采用矩阵做幂运算，其实原理和快速幂差不多，只是需要对矩阵的乘法运算去做*运算符的重载。


    /**
     * 矩阵乘法（重载*）
     * 位运算(转换成二进制处理)
     *
     * @param m
     * @param n
     * @return
     */
    public static int[][] Multiply(int[][] m, int[][] n) {

        /**
         * 对于斐波那契数列来说，行和列都是2，这样写更易于理解，下面也给出了标准的矩阵乘法算法，是通用的
         * 用到此算法，除非进行算法学习和研究，否则一般都是进行较大数据的斐波那契求值，所以对结果取(10e9)+7的模
         * */
        int[][] r = new int[2][2];
        r[0][0] = (m[0][0] * n[0][0] + m[0][1] * n[1][0]) % 1000000007;
        r[0][1] = (m[0][0] * n[0][1] + m[0][1] * n[1][1]) % 1000000007;
        r[1][0] = (m[1][0] * n[0][0] + m[1][1] * n[1][0]) % 1000000007;
        r[1][1] = (m[1][0] * n[0][1] + m[1][1] * n[1][1]) % 1000000007;

        return r;
    }

    /**
     * 矩阵乘法（重载*）
     * 标准计算
     *
     * @param m
     * @param n
     * @return
     */
    public static int[][] MultiplyStandard(int[][] m, int[][] n) {
        int rows = m.length;
        int cols = n[0].length;
        int[][] r = new int[rows][cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                r[i][j] = 0;
                for (int k = 0; k < m[i].length; k++) {
                    r[i][j] += m[i][k] * n[k][j];
                }
            }
        }
        return r;
    }

四、求Fibonacci 第n项

为了正确高效的计算斐波那契数列，我们首先需要了解以下这个矩阵等式：

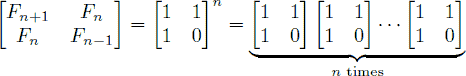
推导这个等式，首先有

[1110][Fn−1Fn]=[Fn+1Fn]\left[ \begin{matrix} 1 & 1\\ 1 & 0 \end{matrix} \right] \left[ \begin{matrix} F_{n-1} \\ F_{n} \end{matrix} \right] = \left[ \begin{matrix} F_{n+1} \\ F_{n} \end{matrix} \right]

然后得到

[Fn+1Fn]=[1110]n[F1F0]\left[ \begin{matrix} F_{n+1} \\ F_{n} \end{matrix} \right] = \left[ \begin{matrix} 1 & 1\\ 1 & 0 \end{matrix} \right]^n \left[ \begin{matrix} F_1 \\ F_0 \end{matrix} \right]

即等于

[FnFn−1]=[1110]n[F0F−1]\left[ \begin{matrix} F_{n} \\ F_{n-1} \end{matrix} \right] = \left[ \begin{matrix} 1 & 1\\ 1 & 0 \end{matrix} \right]^n \left[ \begin{matrix} F_0 \\ F_{-1} \end{matrix} \right]

可得到

[Fn+1FnFnFn−1]=[1110]n[F1F0F0F−1]\left[ \begin{matrix} F_{n+1}&F_{n} \\ F_{n}&F_{n-1} \end{matrix} \right] = \left[ \begin{matrix} 1 & 1\\ 1 & 0 \end{matrix} \right]^n \left[ \begin{matrix} F_1&F_0 \\ F_0&F_{-1} \end{matrix} \right]

所以

[Fn+1FnFnFn−1]=[1110]n\left[ \begin{matrix} F_{n+1}&F_{n} \\ F_{n}&F_{n-1} \end{matrix} \right] = \left[ \begin{matrix} 1 & 1\\ 1 & 0 \end{matrix} \right]^{n}

如此一来，计算斐波那契数列的问题就转化为了求公式矩阵的n-1次幂的问题，并应用快速幂加速计算。

五、完整Java实现

package other;

import java.util.Scanner;

/**
 * @description: 矩阵算法
 * @author: wuyanbo
 * @create: 2019-11-01 10:51
 **/

public class FibonacciMain {


    // Q公式矩阵
    private static final int[][] UNIT = {{1, 1}, {1, 0}};
    // 零矩阵
    private static final int[][] ZERO = {{0, 0}, {0, 0}};

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int[][] m = fb(n);
        System.out.println(m[0][1]);
    }

    /**
     * 递归
     * 求斐波那契数列
     */
    public static int[][] fb(int n) {
        if (n == 0) {
            return ZERO;
        }
        if (n == 1) {
            return UNIT;
        }
        if (n % 2 == 0) {
            int[][] matrix = fb(n >> 1);
            return Multiply(matrix, matrix);
        } else {
            int[][] matrix = fb((n - 1) >> 1);
            return Multiply(Multiply(matrix, matrix), UNIT);
        }

    }

    /**
     * 矩阵乘法
     * 位运算转换成二进制处理
     *
     * @param m
     * @param n
     * @return
     */
    public static int[][] Multiply(int[][] m, int[][] n) {

        /**
         * 对于斐波那契数列来说，行和列都是2，这样写更易于理解，下面也给出了标准的矩阵乘法算法，是通用的
         * 用到此算法，除非进行算法学习和研究，否则一般都是进行较大数据的斐波那契求值，所以对结果取(10e9)+7的模
         * */
        int[][] r = new int[2][2];
        r[0][0] = (m[0][0] * n[0][0] + m[0][1] * n[1][0]) % 1000000007;
        r[0][1] = (m[0][0] * n[0][1] + m[0][1] * n[1][1]) % 1000000007;
        r[1][0] = (m[1][0] * n[0][0] + m[1][1] * n[1][0]) % 1000000007;
        r[1][1] = (m[1][0] * n[0][1] + m[1][1] * n[1][1]) % 1000000007;

        return r;
    }

    /**
     * 矩阵乘法算法
     * 标准计算
     *
     * @param m
     * @param n
     * @return
     */
    public static int[][] MultiplyStandard(int[][] m, int[][] n) {
        int rows = m.length;
        int cols = n[0].length;
        int[][] r = new int[rows][cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                r[i][j] = 0;
                for (int k = 0; k < m[i].length; k++) {
                    r[i][j] += m[i][k] * n[k][j];
                }
            }
        }
        return r;
    }
}

参考博客ZHENGYI'S BLOG

Copyright © 2020 - 2025 saowu. All Right Reserved
Powered by Gridea